Uji Dua Rata-rata Varian Sama

Pada pembahasan kali ini kita akan menjelaskan mengenai uji dua rata-rata dengan dua varian diasumsikan sama. Uji dua rata-rata dengan dua varian yang diasumsikan sama dilakukan jika nilai varian masing-masing rata-rata yang dibandingkan dianggap sama. Biasanya sebelum dilakukan analisis diawali dengan uji terhadap nilai varian dari kedua rata-rata yang dibandingkan. Jika uji terhadap varian menunjukan non signifikan maka analisis ini dapat diterapkan. Pada ukuran sampel kecil dengan distribusi data mengikuti distribusi normal dan standar deviasi yang tidak diketahui, nilai t dalam uji ini dirumuskan sebagai berikut :

Contoh Kasus :

Konsultan riset sedang meneliti biaya perbaikan dua jenis mobil terbaru dengan tipe sama yang dimiliki oleh dua buah perusahaan otomotif. Karena begitu mahalnya biaya uji diputuskan untuk mobil A menggunakan 5 buah sampel dan mobil B menggunakan 7 buah sampel. Data hasil pengamatan adalah sebagai berikut :

Mobil B
1	100
2	250
3	200
4	600
5	800
6	500
7	200

Mobil A
1	200
2	450
3	790
4	500
5	950

Jika kedua varian biaya perbaikan mobil diasumsikan sama, lakukan analisis apakah kedua biaya perbaikan mobil adalah sama...???

Penyelesaian secara manual

1.       Hipotesis dari kasus biaya perbaikan mobil tersebut adalah

Ho : µ_A = µ_B

Ha : µ_A ≠ µ_B

2.       Hitung nilai rata-rata

3.       Hitung nilai standard deviasi

4.       Hitung nilai  

5.     Tentukan t tabel pada α/2 dan derajat bebas (df = n1+n2-2=10)

Nilai t(0,05/2,10) = 2,2281139

6.       Hitung nilai confident interval of different (D)

7.      Hitung nilai t

8.      Pengambilan keputusan

Karena nilai interval D melalui titik 0 dan nilai t hitung < t tabel, maka Ho diterima dan Ha ditolak. Dengan demikian, dapat disimpulkan bahwa pada tingkat kepercayaan 95% biaya perbaikan kedua mobil tidak berbeda nyata.

Penyelesaian dengan MS Excel

1.       Susun data input seperti tampilan berikut :

2.       Klik menu Data pada Toolbars, lalu klik Data Analysis. Akan tampil jendela Data Analysis

3.       Pilih t-Test : Two-Sample Assuming Equal Variances, lalu OK

4.       Maka akan muncul jendela Two-Sample Assuming Equal Variances

5.     Variabel 1 Range menyatakan input untuk variabel Mobil A (data input $A$1:$A$6) dan variable 2 Range menyatakan input untuk mobil B (data input $B$1:$B$8).

6.      Aktifkan Labels, isi Hypothesized Mean Difference dengan 0,05 (alpha) dan Output Range letakan pada Cell D1 dengan mengetik $D$1 lalu klik OK.

Maka akan tampil sebagai berikut :

7.   Nilai Mean menyatakan nilai rata-rata aritmetik masing-masing jenis mobil. Nilai rata-rata biaya perbaikan mobil A adalah sebesar $578 dan mobil B $378,571. T-stat menyatakan t hitung sebesar 1,24534, t critical two-tail menyatakan t tabel dengan nilai 2,228139

Penyelesaian dengan SPSS 17

1.  Berbeda dengan penulisan data pada analisis sebelumnya, maka pada t test, variabel dibedakan menjadi dua bagian, yaitu variabel Jenis_Mobil dan variabel pengukuran kita namakan Biaya. Variabel Jenis_mobil bertipe string, sedangkan variabel biaya berupa numeric.

2.       Pada variabel jenis_mobil klik bagian values isi dengan nilai 1 (Mobil A) klik Add dan isi dengan nilai 2 (Mobil B) dan klik Add, hasilnya seperti berikut :

3.       Klik OK lalu klik Data View, lalu klik menu View pada Toolbars, kemudian aktifkan Value Label dengan cara mengkliknya.

4.       Pada kolom variabel jenis_mobil ketikan 1 sebanyak 5 kali (n1 = 5), kemudian 2 sebanyak 7 kali (n2 = 7).

5.  Pada kolom biaya isikan sesuai urutan data yang ada di tabel contoh soal. Jika benar hasil pengisiannya terlihat seperti berikut :

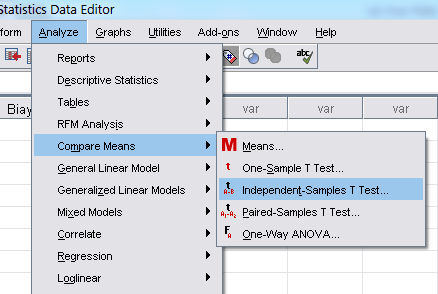
6.       Klik menu Analyze pada Toolbars lalu pilih Compare Means kemudian Independent-Samples T test, maka akan muncul tampilan Independent-Samples T test.

7.       Masukan biaya ke Test Variable(s)

8.       Masukan jenis_mobil ke Goruping Variable.

9.       Klik Define Groups dan isi Group 1 dengan nilai 1 dan Group 2 dengan nilai 2 dan klik continue

10.   Klik options, atur defaultnya seperti berikut :

11.   Setelah semua langkah dilakukan, klik continue dan klik OK, maka hasil nya seperti berikut :

  

12.  Seperti halnya perhitungan sebelumnya, disini diketahui nilai rata-rata biaya perbaikan mobil A adalah sebesar $578 dan mobil B adalah sebesar $378,57 dengan t hitung = 1,245 p(t) = 0,241 dan CI untuk D adalah -$157,384 ≤ D ≤ $556,241 (lihat bagian Lower dan Upper)

13.   Pengambilan keputusan

Karena nilai p(t) > 0,05 dan nilai CIDifference di dalamnya terdapat nol (0), maka Ho diterima dan Ha ditolak. Dengan demikian dapat disimpulkan bahwa biaya perbaikan kerusakan mobil A dan mobil B adalah tidak berbeda nyata pada tingkat keyakinan 95%.

Demikian tutorial Uji dua rata-rata dengan dua varian yang diasumsikan sama, semoga tutorial ini dapat bermanfaat.